Applied Information Economics (AIE)
Measure what Matters, Make better Decisions
A decision is only as good as the data and analysis on which it is based. Our proprietary quantitative analytical method, Applied Information Economics, provides a proven, scientific framework for measuring anything and using the results to make more informed – and better – decisions.
An Overview of Applied Information Economics
Applied Information Economics (AIE) is a synthesis of techniques from economics, actuarial science, and other mathematical methods (see Figure 1). AIE employs methods that are proven by a large body of peer-reviewed academic research and empirical evidence on improving human expert judgments.
Even though AIE was based on academic support and evidence, it is a practical approach that helps HDR clients every day in a variety of real industry, government, and humanitarian efforts. We have implemented AIE in to over 200 major decision portofolios.
Some of the basic techniques that make AIE a powerful set of tools include a method for clarifying decisions and defining variables in a quantitative way, calculation methods for the value of information, methods for modeling uncertainty as estimates, measurement methods, and treating the decision as a choice among different investment portfolios. These methods are part of a formalized procedure that includes the following major activities:
- Define the Decision(s): We help our clients identify the real decision at the outset. Is the dilemma whether to simply approve a project or how to conduct a project given a vast combination of alternatives? Or is the decision a matter of when a given initiative should be approved? The costs, benefits, timing, risks and even external factors are identified and the real decision is clarified
- Model What We Know Now: Cost estimates, market forecasts, project risks, and other variables in a typical big investment decision are almost never known exactly. Usually, the uncertainty about some variables, especially long term forecasts, can seem extreme. But even extremely uncertain variables can be assessed using HDR’s methods. AIE uses methods to compensate for the natural overconfidence and the inconsistency of most managers and decision makers. This results in measurably better forecasts and decisions. These methods are shown to work even when organizations have very little historical data, complex problems, and measurements that seem almost impossible.
- Measure What Matters: AIE’s unique approach to uncertain decisions involves picking the right things to measure. Not all variables in a decision are worth measuring and those worth measuring are often a surprise to the decision makers. In fact, most managers measure exactly the wrong things – that is, the most uncertain variables tend to be ignored while the variables that usually receive a lot of attention actually have less bearing on the decision. With AIE, every variable in a model will have an “information value” that allows identification of high value variables in a decision.
- Make Better Decisions: This can include decisions that are more than just “accept/reject” choices but possible combinations of several choices. The final outcomes must consider the risk preferences of decision makers. The output of the decision model, updated with economically justified measurements, is compared to the risk appetite of the organization.
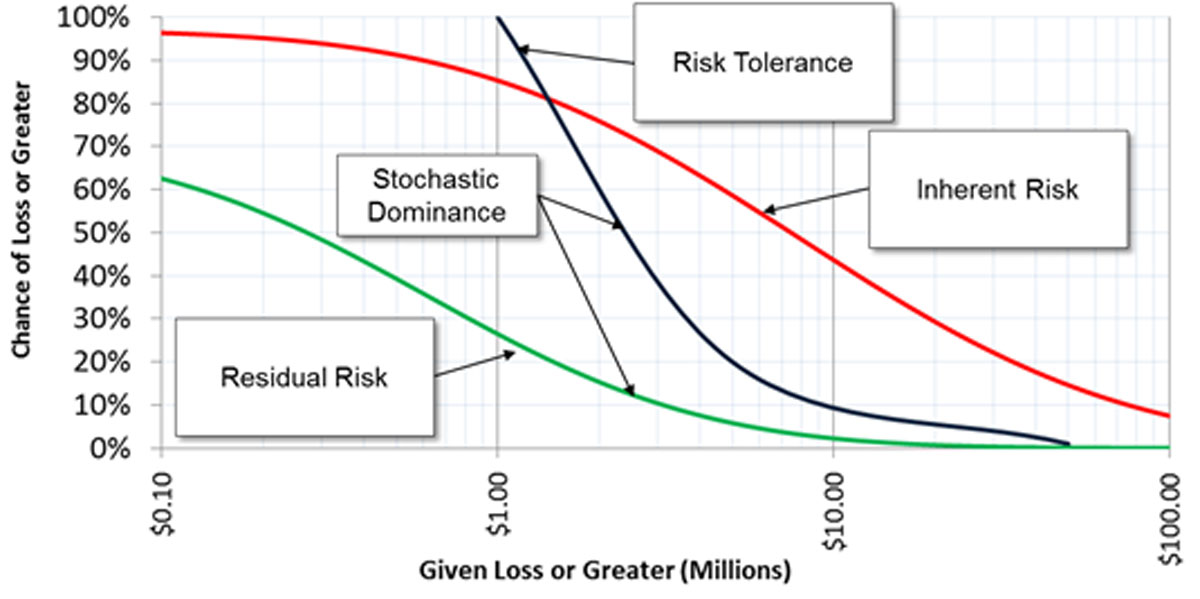
The output of this process is not a point scale or “high, medium, low” rating. AIE produces results that would be familiar to actuaries and quantitative financial analysts. For ERM, portfolio risk is illustrated with what is known as a Loss Exceedance Curve (LEC). As Figure 2 illustrates, we would generate an initial or “inherent” risk curve and a subsequent “residual risk” curve after risk mitigations are employed.
Both curves are compared to a “risk tolerance” curve to determine if a proposed action imposes or mitigates risks to within a level deemed to be acceptable to management. The inherent risk curve (in red) shows that, prior to risk mitigation actions, there was a 45% chance of losing more than $10 million in each year and an 8% chance of losing more than $100 million. This is much more exposure to loss than management will accept, as shown by the risk tolerance curve (in black). After mitigating actions are taken, the residual risk curve (in green) is entirely below the risk tolerance curve.
By taking a mathematically sound approach, this allows us to compute a “Return on Control” (RoC) for each proposed risk mitigation. The spreadsheet will be able to show expected RoC for many mitigations at once so that control priorities can be determined.
The Need for a Better Approach
Some of the most important decisions that must be made for businesses and governments to progress are surrounded by the unknown. Many business choices are ones tied with high uncertainty and many factors seem immeasurable such as economic value, performance, quality, and risk.
If you are an executive in a position to make big decisions in your organization, you probably have asked yourself many of the following questions:
- How can I compute a return on an investment if most of the benefits seem “intangible”?
- How do I measure and manage risk when there is little historical data on this kind of investment?
- How do I calculate the economic value of more, better, or faster information?
- Is there any alternative to our subjective and politically driven decision process?
Figuring out these answers can be a challenge but with the Applied Information Economics method, these questions, and more, can be answered easily and with top-notch results.
The AIE Solution
Applied Information Economics (AIE) is the first truly scientific and theoretical method developed for addressing the dilemmas even when it may seem like there is no way to measure the problem, such as with economic value. Applied Information Economics uses methods that show independently, scientifically measured improvements to management forecasts and decisions. Concepts that seemed like intangibles, now have proven economic formulae to help your business drive results.
Applied Information Economics combines methods of Game theory, Decision theory, economics, quantitative risk analysis, operations research, and Modern Portfolio theory to create an analysis on measuring what matters. Applied Information Economics adds economic value to information that is obscured by uncertainty and implements targeted measurement efforts. The AIE method has been widely used in many practical business environments including insurance, manufacturing, transportation, utilities, banking, .com startups, and media. Applied Information Economics is a complete-solution methodology that includes training, tools, process documentation, and initial consulting. All measurements are real measurements that are based on proven methods and have a known statistical validity.
AIE provides a measurable improvement for management decisions for subjects such as economic value. Contact Hubbard Decision Research today so you can make important choices for your business through the Applied Information Economics method.
