
During the course of a typical day, humans will make an enormous amount of conscious and subconscious decisions. Not all of those decisions are what we’d call crucial. The vast majority aren’t. But every day, we’ll make several decisions that matter – that have a significant impact on how our lives unfold.
When we’re trying to decide on a course of action from the multitude of options we typically have, we’re trying to, at the very least, predict the future. (Not in an psychic sense, of course.) In other words, we’re assessing the options we have and calculating the probability that decision A will result in outcome A, B, or C – while also figuring out how good or bad outcomes A, B, or C would be if they happened.
Of course, we all want to make good decisions. But we don’t always do that – and sometimes, our bad decisions are catastrophic.
As we’re about to cover, there are several reasons why humans make poor decisions, ranging from cognitive biases to simply not using the right processes. We’ll also cover what you can do to put yourself in a position to make better calls and do a better job of predicting outcomes and assessing probabilities.
The takeaway will be simple: If you do the right things, your decision-making ability will measurably improve – and a good number of those bad decisions can be changed for the better.
A Decision-Maker’s Most Formidable Foe: Uncertainty
Think about some of the decisions you’ve had to make in your life.
If you went to college, you had to pick one. If you’re married, or engaged, you had to find a partner and decide to propose – or accept a proposal. In your job, maybe you had to decide what investment to make, or what actions to take. If you’re a business owner, you had to make a ton of important decisions that led to where you are today, for better or for worse.
In every single one of those decisions, you didn’t know for sure what would happen. Even if you thought it was a 100% sure thing, it probably wasn’t, because there are few sure things in the world. When there is more than one possible outcome, and you’re not sure which one will occur, you experience something called uncertainty, and it can be quantified on a 0-100% scale (such as being 90% sure your partner is going to say yes to your proposal, or only 50% sure – the same as a coin flip – that your big investment is going to pay off.)
Usually, hard decisions – the decisions that determine success versus failure – involve dozens of variables that lead to multiple possible outcomes. With each variable and potential outcome comes a great deal of uncertainty – so much at times, in fact, that it’s a wonder decisions are made at all.
In short, we deal with uncertainty every single day, with every decision we make. The tougher the decision, the more uncertainty – or, should we say, the more uncertainty, the tougher the decision.
Being better at assessing probabilities, making decisions, and predicting the future is all about reducing uncertainty as much as possible. If you can reduce the amount of uncertainty you face, whether you’re figuring out how likely something is to happen or trying to predict what will happen in the future, you’ll be more likely to make the right call.
The trouble is, humans are bad at assessing probabilities and predicting the future. Research has shown why this is the case. Daniel Kahneman, with Amos Tversky, won a Nobel Prize in Economics for showing how humans are subject to a wide array cognitive biases based on how much we rely on erroneous judgmental heuristics.
Researchers Baruch Fischhoff, Paul Slovic, and Sarah Lichtenstein found that humans are psychologically biased toward unwarranted certainty, i.e. we tend to be overconfident when we make judgments due to a variety of reasons, such as our memories being incomplete and erroneously recalled. Put another way, we are often extremely overconfident when we think we’re right about something, especially when we rely on our experience (or rather, our perceptions of that experience).
Psychologist and human judgment expert Robyn Dawes confirmed the effect of these limitations when he found that expert judgment is routinely outperformed by actuarial science (i.e. hard quantitative analysis) when it came to making decisions.
Social psychologists Richard Nisbett and Lee Ross explained how “Stockbrokers predicting the growth of corporations, admissions officers predicting the performance of college students, and personnel managers choosing employees are nearly always outperformed by actuarial formulas.”
Put together, there are many reasons why we, as a species, are not terribly good at figuring out what is going to happen and how likely it is to happen. When you’re trying to make decisions in a world of uncertainty – i.e. every time you try to make a decision – you’re fighting against your brain.
Does that mean we should just concede to our innate biases, misconceptions, and flaws? Does it mean that there’s no real way to improve our ability to reduce uncertainty, mitigate risk, and make better decisions?
Fortunately for us, there are ways to get better at assessing how likely something is to happen, reducing uncertainty, and giving yourself a better chance at making the right call.
Calibration: Making Yourself a Probability Machine
In May, 2018, the United States Supreme Court struck down a federal ban on sports betting. Before that decision, only four states allowed sports betting in any capacity. Since the decision, most states have either legalized sports betting, passed a bill to do so, or introduced a bill to make betting legal within their boundaries.
When we bet on sports, we’re essentially predicting the future (or as Doug says, trying to be less wrong). We’re saying, “I will wager that the New England Patriots will beat the New York Jets,” or that “The Houston Rockets will lose to the Golden State Warriors but only by less than five points.”
When we place a bet, we’re gambling that our confidence in the outcome we’re predicting is better than 50/50, which is a coin flip. Otherwise, there’s no point in making a bet. So, in our heads, we think, “Well, I’m pretty sure New England is the better team.” If we’re the quantitative type, we try to put a percentage to it: “I’m 70% confident that the Rockets can keep it close.”
Putting a percentage on uncertainty is good; the first step when reducing uncertainty is to quantify it. But simply slapping an arbitrary number on your confidence creates problems, namely, how accurate is your number?
In other words, if you’re 70% confident, the event should happen 70% of the time. If it happens more frequently, you were underconfident; if it happens less frequently (as is usually the case), then you were overconfident and could potentially lose a lot of money.
The range of probable values that you create to quantify your uncertainty is called a confidence interval (CI). If you’re betting on sports – or anything, really – then you can quantify uncertain by giving yourself a certain range of possibilities that you think are likely depending on your confidence.
For example, let’s say that Golden State is predicted by Vegas bookies to beat Houston by 5 or more points. You think, “Well, there’s no way they lose, so the minimum amount they’ll win by is one point, and they could really blow Houston out, so let’s say the most they’ll win by is 12 points.” That’s your range. Let’s say you think you’re 90% confident that the final margin of victory will be within that range. Then, you are said to have a 90% CI of one to 12.
You’ve now quantified your uncertainty. But, how do you know your numbers or your 90% CI are good? In other words, how good are you at assessing your own confidence in your predictions?
One way to figure out if someone is good at subjective probability assessments is to compare expected outcomes to actual outcomes. If you predict that particular outcomes will happen 90% of the time, but they only happened 80% of the time, then perhaps you were overconfident. Or, if you predict that outcomes will happen 60% of the time, but they really happened 80% of the time, you were underconfident.
This is called being uncalibrated. So, it follows that being more accurate in your assessments is being calibrated.
Calibration basically is a process by which you remove estimating biases that interfere with assessing odds. This process has been a part of decision psychology since the 1970’s, yet it’s still relatively unknown in the broader business world. A calibrated person can say that an event will happen 90% of the time, and 90% of the time, it’ll happen. They can predict the outcome of 10 football games with a 90% CI and hit on 90% of them. If they say they’re 90% sure that the Patriots will beat the Jets, they can make a bet and 90% of the time, they’ll be right.
More broadly speaking, a calibrated person is neither overconfident or underconfident when assessing probabilities. This doesn’t mean the person is always right; they won’t be. (Doug Hubbard talks about how a 90% CI is more useful than a 100% CI, or saying the outcomes outside of your range absolutely won’t happen, which isn’t often the case in the real world). It just means that they are better at estimating probabilities than other people.
Put very simply, as Doug does in his book, How to Measure Anything, “A well calibrated person is right just as often as they expect to be – no more, no less. They are right 90% of the time they say they are 90% confident and 75% of the time they say they are 75% confident.”
The unfortunate news is that the vast majority of people are uncalibrated. Very few people are naturally good at probabilities or predicting the future.
The fortunate news is that calibration can be taught. People can move from uncalibrated to calibrated through special training, such as our calibration training, and it’s easier than you think.
Consider the image below (Figure 1). This is a list of questions and statements from our calibration training sessions we offer. The top half contains a list of 10 trivia questions. We ask participants to give us a 90% CI – i.e. a range of values in which they’re 90% sure the correct answer will be. So, for the first question, a participant may be 90% certain that the actual answer is anywhere from 20 mph to 400 mph.
For the second list, we ask participants to answer true or false and mark their confidence that they are correct.
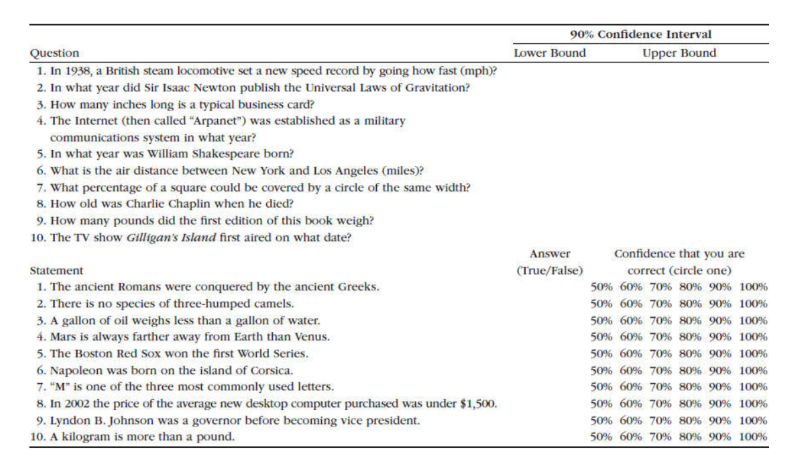
Figure 1: Sample of Calibration Test
Some of those questions may be very difficult to answer. Some might be easy. Whether you know the right answer or not isn’t the point; it’s all about gauging your ability to assess your confidence and quantify your uncertainty.
After everyone is finished, we share the actual answers. Participants get to see how well their assessments of their confidence stack up. We then give feedback and repeat this process across a series of tests that we’ve designed.
What most people find is that they are very uncalibrated, and usually quite overconfident. (Remember from earlier the research that shows how people tend to be naturally overconfident in their assessments and predictions). We also find people that are underconfident.
Over the course of the training session, however, roughly 85% of participants will become calibrated, in that they’ll hit on 90% of the questions. That’s because during the training, we share with them several proven techniques that they can use throughout the testing to help them make better estimates.
A combination of technique and practice, with feedback, results in calibration. As you can see in the image below (Figure 2), calibrated groups outperform uncalibrated groups when evaluating their confidence in predicting outcomes.
 Figure 2: Comparison of Uncalibrated versus Calibrated Groups
Figure 2: Comparison of Uncalibrated versus Calibrated Groups
Long story short, calibration is a necessary part of making subjective assessments of probabilities. You can’t avoid the human factor in decision-making. But you can reduce uncertainty and your chance of error by getting better at probabilities by becoming calibrated, which means your inputs to a decision-making model will be more useful.
Quantitative Tools to Help Make Better Decisions
Calibration alone won’t turn you into a decision-making prodigy. To go even further, you need numbers – but not just any numbers and not just any method to create them.
The use of statistical probability models in decision-making today is a relatively new thing. The field of judgment and decision-making (JDM) didn’t emerge until the 1950’s, and really took off in the 1970’s and 1980’s through the work of Nobel laureate Daniel Kahneman (most recently the author of bestseller Thinking Fast and Slow) and his collaborator, Amos Tversky.
JDM is heavily based on statistics, probability, and quantitative analysis of risks and opportunities. The idea is that a well-designed quantitative model can remove many of the cognitive biases that are innate to mankind that interfere with making good decisions. As mentioned previously, research has borne that out.
One striking example of how statistics evolved in the 20th Century to allow analysts to make better inferences came during World War II, as told by Doug in How to Measure Anything. The Allies were very interested in how many Mark V Panther tanks Nazi Germany could produce, since armor was arguably Germany’s most dominant weapon (alongside the U-boat) and the Mark V was a fearsome weapon. They needed to know what kind of numbers they’d face in the field so they could prepare and plan.
At first, the Allies had to depend on spy reports. These are very inconsistent. Allied intelligence cobbled together these reports and came up with estimates of monthly production ranging from 1,000 in June 1940 to 1,550 in August 1942.
In 1943, however, statisticians took a different approach. They used a technique called serial sampling to sample tank production using the serial numbers on captured tanks. As Doug says, “Common sense tells us that the minimum tank production must be at least the difference between the highest and lowest serial numbers of captured tanks for a given month. But can we infer even more?”
The answer was yes. Statisticians treated the captured tank sample as a random sample of the entire tank population and used this to compute the odds of different levels of production.
Using these statistical methods, these analysts were able to come up with dramatically different – and far more accurate – tank production estimates than what Allied intelligence could produce from its earlier reports (see Figure 3).
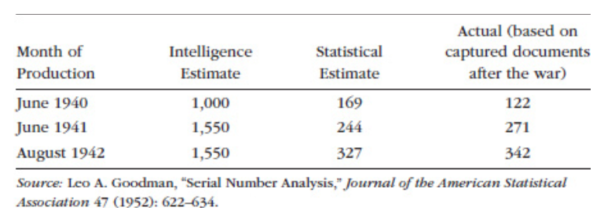
Figure 3: Results of the Serial Number Analysis
The military would go on to become a believer in quantitative analysis, which would spread to other areas of government and also the private sector, fueled by the emergence of computers that could handle increasingly-sophisticated quantitative models.
A Sampling of Quantitative Tools and Models
Today, a well-designed quantitative model takes advantage of several key tools and methods that collectively do a better job of analyzing all of the variables and potential outcomes in a decision and informing the decision-maker with actionable insight.
These tools include:
- Monte Carlo simulations: Developed during World War II by scientists who were working on the Manhattan Project, Monte Carlo simulations analyzes risks through modeling all possible results via repeated simulations using a probability distribution. Thousands of samples are generated to create a range of possible outcomes to give you a comprehensive picture of not just what may occur, but how likely it is to occur.
- Bayesian analysis: Named for English mathematician Thomas Bayes, Bayesian analysis combines prior information for a parameter (or variable) with a sample to produce a range of probabilities for that parameter. It can be easily updated with new information to produce more relevant probabilities.
- Lens Method: Developed by Egon Brunswick in the 1950’s, this method measures and removes significant sources of errors in expert judgments due to estimator inconsistency through a regression model.
- Applied Information Economics (AIE): AIE combines several methods from economics, actuarial science, and other mathematical disciplines to define the decision at hand, measure the most important variables and factors, calculate the value of additional information, and create a quantitative decision model to inform the decision-maker.
The result of all methods put together is a model, which can take data inputs and produce a statistical output that helps a decision-maker make better decisions.
Of course, the outputs are only as good as the inputs and the model itself, and not all inputs are important. The model, first, has to be based on sound mathematical and scientific principles. Second, the inputs have to be useful – but most of them aren’t. This is a concept Doug Hubbard calls measurement inversion (see Figure 4).

Figure 4: Measurement Inversion
Put simply, decision-makers and analysts think certain variables are important and should be measured, and ignore other variables that are deemed as unimportant or immeasurable. Ironically, the variables they think are relevant usually aren’t, and the ones they think aren’t relevant are usually the things they most need to measure.
In Figure 5, you can see real-world examples of measurement inversion, as uncovered through the past 30 years of research Hubbard Decision Research has conducted.
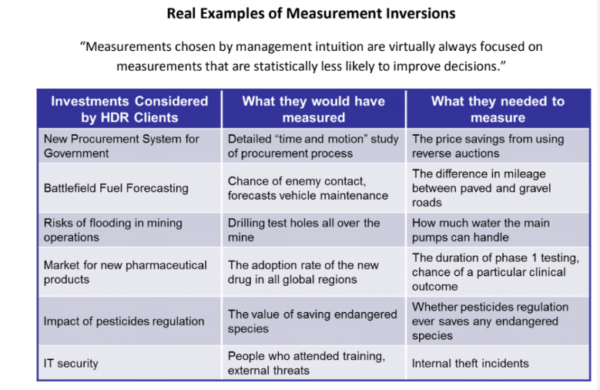
Figure 5: Real-World Examples of Measurement Inversion
These and other cases of measurement inversion have been backed by research and statistical analysis. What’s often the case is that a decision-maker is basing decisions on outputs from a model that is either not sound, or – more dangerously – is sound yet is getting fed erroneous or irrelevant data.
One thing AIE does is calculate the value of information. What’s it worth to us to take the effort to measure a particular variable? If you know the value of the information you have and can gather, then you can measure only what matters, and thus feed your model with better inputs.
With the right inputs, and the right model, decision-makers can make decisions that are measurably better than what they were doing before.
Conclusion: Making Better Decisions
If a person wants to become better at making decisions, they have to:
- Recognize their innate cognitive biases;
- Calibrate themselves so they can get better at judging probabilities; and
- Use a quantitative method which has been shown in published scientific studies to improve estimates or decisions.
The average person doesn’t have access to a quantitative model, of course, but in the absence of one, the first two will suffice. For self-calibration, you have to look back at previous judgments and decisions you’ve made and ask yourself hard questions: Was I right? Was I wrong? How badly was I wrong? What caused me to be so off in my judgment? What information did I not take into consideration?
Introspection is the first step toward calibration and, indeed, making better decisions in general. Adopting a curious mindset is what any good scientist does, and when you’re evaluating yourself and trying to make better decisions, you’re essentially acting as your own scientist, your own analyst.
If you’re a decision-maker who does or can have access to quantitative modeling, then there’s no reason to not use it. Quantitative decision analysis is one of the best ways to make judgment calls based on empirical evidence, instead of mere intuition.
The results speak for themselves: decision-makers who make use of the three steps outlined above really do make better decisions – and you can actually measure how much better they are.
You’ll never be able to gaze into a crystal ball and predict the future with 100% accuracy. But, you’ll be better at it than you were before, and that can make all the difference.

