The American Statistician Presents the Most Important Improvement to Scientific Method in Over 80 Years
 Science, we have a problem. Several problems, actually. Now we have solutions. A central tenant of modern science is that experiments must be reproducible. It turns out that a surprisingly large proportion of published results in certain fields of research – especially in the social and health sciences – do not satisfy that requirement. This is known as the reproducibility crisis.
Science, we have a problem. Several problems, actually. Now we have solutions. A central tenant of modern science is that experiments must be reproducible. It turns out that a surprisingly large proportion of published results in certain fields of research – especially in the social and health sciences – do not satisfy that requirement. This is known as the reproducibility crisis.
I was honored to have the opportunity to be involved in addressing this as both an associate editor of a ground-breaking special Issue of The American Statistician and to co-author one of the 43 articles. This special issue is called “Moving to a World Beyond p<.05” Some of my readers will recognize that “p<.05” refers to the “significance test”, ubiquitous in scientific research. This issue is the first serious attempt to fundamentally rethink statistical inference in science since the significance tests currently used were developed almost a century ago.
The article I authored with Alicia Carriquiry (Distinguished Professor of Statistics at Iowa State University) is titled Quality Control for Scientific Research: Addressing Reproducibility, Responsiveness, and Relevance. We argue that addressing responsiveness and relevance will help address reproducibility. Responsiveness refers to the fact it takes a long time before problems like this are detected and announced. The discovery of the current problems of reproducibility only occurred because, periodically, some diligent researchers decided to investigate it. Years of unreproducible studies continue to be published before these issues are known and even longer before they are acted on.
Relevance refers to how published research actually supports decisions. If the research is meant to inform corporate or public decisions (it is certainly often used that way) then it should be able to tell us the probability that the findings are true. Assigning probabilities to potential outcomes of decisions is a vital step in decision theory. Many who have been using scientific research to make major decisions would be surprised to learn that the “Null Hypothesis Significance Test” (NHST) does not actually tell us that.
However, Alicia and I show a proof about how this probability could be computed. We were able to show that we can compute the relevant probability (i.e., that the claim is true) and that even after a “statistically significant” result the probability is, in some fields of research, still less than 50%. In other words, a “significant” result doesn’t mean “proven” or even necessarily “likely.” A better interpretation would be “plausible” or perhaps “worth further research.” Only after the results are reproduced does the probability the hypothesis is true start to grow to about 90%. This would be disappointing for policy makers or news media that tend to get excited about the first report of statistical significance. In fact, measuring such probabilities can be the basis of a sort of quality control for science that can be much more responsive as well as relevant. Any statistically significant result should be treated as a tentative finding awaiting further confirmation.
Now, a little background to explain what is behind such an apparently surprising mathematical proof. Technically, a “statistically significant” result only means that if there were no real phenomena being observed (the “null” hypothesis) then the statistical test result – or something more extreme – would be unlikely. Unlikely in this context means less than the stated significance level, which in many of the research fields in question is 0.05. Suppose you are testing a new drug that, in reality, is no better than a placebo. If you would have run an experiment 100 times you would, by chance alone, get a statistically significant result in about 5 experiments at a significance level of .05. This might sound like a tested hypothesis with a statistically significant result has a 95% chance of being of being true. It doesn’t work that way. First off, if you only publish 1 out of 10 of your tests, and you only publish significant results, then half of your published results are explainable as chance. This is called “publication bias.” And if a researcher has a tendency to form outrageous hypotheses that are nearly impossible to be true, then virtually all of the significant results would be the few random flukes we would expect by chance. If we could actually compute the probability the claim is true, then we would have a more meaningful and relevant test of a hypothesis.
One problem with answering relevance is that it requires a prior probability. In other words, we have to have to be able to determine a probability the hypothesis is true before the research (experiment, survey, etc.) and then update it based on the data. This reintroduces the age-old debate in statistics about where such priors come from. It is sometimes assumed that such priors can only be subjective statements of an individual, which undermines the alleged objectively of science (I say alleged because there are several arbitrary and subjective components of statistical significance tests). We were able to show that an objective prior can be estimated based on rate at which studies in a given field can be successfully reproduced.
In 2015, a group called The Open Science Collaboration tried to reproduce 100 published results in psychology. The group was able to reproduce only 36 out of 100 of the published results. Let’s show how this information is used to compute a prior probability as well as the probability the claim is true after the first significant results and after it is reproduced.
The proposed hypothesis the researcher wants to test the truth of is called “alternative” to distinguish it from the null hypothesis, where the results were a random fluke. The probability that the alternative hypothesis is true, written Pr(Ha), based only on the reproducibility history of a field, is:
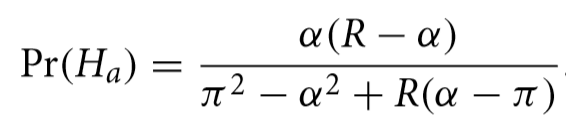
Where R is the reproducibility rate, and α and π refer to what is known as the “significance level” and the statistical “power” of the test. I won’t explain those in much detail but these would be known quantities for any experiment published in the field.
Using the findings of The Open Science Collaboration, R would be .36 (actually we would use those results as a sample to estimate the reproduction rate which itself would have an error, but we will gloss over that here). The typical value for α is .05 and π is, on average, perhaps as high as .8. This means that that hypothesis being considered for publication in that field have about a 4.1% chance of being true. Of course, you would expect that researchers proposing a hypothesis probably have reason to believe they have some chance that what they are testing is true but before the actual measurement, the probability isn’t very high. After the test is performed, the following formula shows the probability is a claim is true given that it passed the significance test (shown as the condition P< α).
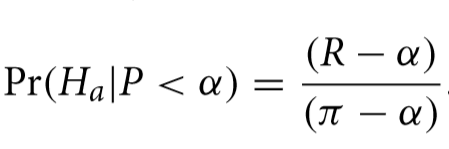
What might surprise many decision makers who might want to act on these findings that that, in this field of research, a “significant” result using an experiment with the same α and π means that now we can say that the hypothesis has only a 41.3% chance of being true. When (and if) the result is ever successfully reproduced it, the probability the hypothesis is true is adjusted again to 91.9% with the following formula.
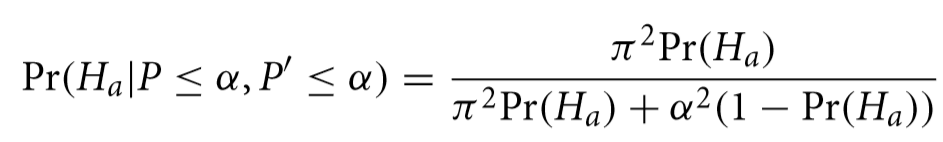
If we plot all three of these probabilities as a function of reproduction rate for a given α and π, we get a chart like the following.
Probability the hypothesis is true upon initial proposal, after the first significant result and after reproduction
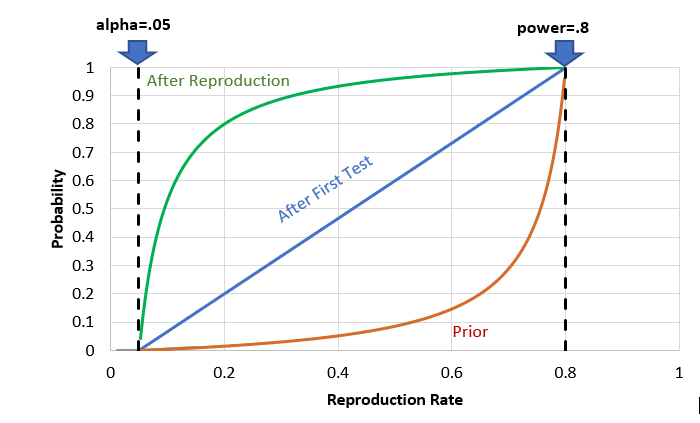
Other reproduction attempts similar to The Open Science Collaboration show replication rates well short of 60% and more often below 50%. As the chart shows, if we wanted to have a probability of at least 90% that a hypothesis is true before making a policy decision, reproduction rates would have to be on the order of 75% or higher holding other conditions constant. In addition to psychology, these findings affect issues as broad as education policy, public health, product safety, economics, sociology, and many other fields where significance tests are normal practice.
Alicia and I proposed that Pr(Ha) itself becomes an important quality control for fields of research like psychology. Instead of observing problems perhaps once every decade or two, Pr(Ha) can be updated with each new reproduction attempt and that will update all of the Pr(Ha|P<a) in the field at a rate closer to real time. Now, our paper is only one of 43 articles in this massive special issue. There are many articles that will be very important in rethinking how statistical inference has been applied for many decades.
The message across all the articles is the same – the time for rethinking quality control in science is long overdue and we know how to fix it.
– Doug Hubbard

