
The Diamond Princess cruise ship is currently under quarantine while 271 passengers are being tested (as of 2/5/2020) for the 2019 novel coronavirus (2019 n-CoV). Concern about infection arose when a prior passenger from Hong Kong who was on board the ship from 1/20 to 1/25 was later found to be infected. As a result, the ship was delayed and then quarantined off the port of Yokohama to test a group of 271 passengers who either had symptoms of 2019 n-CoV or had significant contact with the original case from Hong Kong. On Wednesday (2/5) 10 out of 31 tests had come back positive from a suspected 271 people. By Thursday, 20 out of 102 tests had come back positive. This is a real world application where we can test the utility of a Beta distribution to predict an outcome – we shouldn’t be surprised if another 15-46 people test positive for the coronavirus out of the remaining tests.
A Beta distribution for the first 31 tests would have an alpha of 11 (10+1) and a beta of 22 (21+1); the 90% confidence interval for the proportion using the first sample is 21%-47% (Figure 1). The second group of tests has an alpha of 11 (10+1) and a beta of 62 (61+1); the 90% confidence interval for the proportion given this sample is 9%-22% (Figure 1). Based on these results, we suspect that they tested the more likely cases first, and the remaining 169 are more likely to resemble the second sample in likelihood of infection. However, if the first two samples were randomly selected then we would use the beta distribution of all 102 initial cases (alpha = 21, beta = 83) with a 90% C.I. of 14 to 27%.
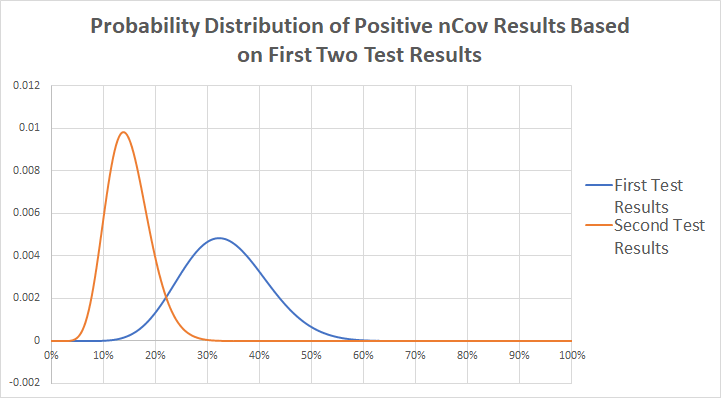
Figure 1: Difference in distributions between the first and second sets of test results
Since we don’t know which is accurate, we’ll use 9-27% for our 90% confidence interval, which gives us an estimate of 35 to 66 total of this group of 271 will test positive for the coronavirus (Figure 2). This would imply that an additional 15 to 46 positive results will come back from the remaining 169 tests.
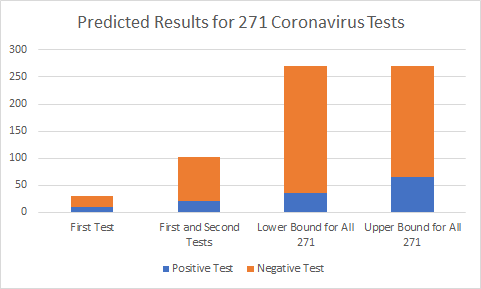
Figure 2: Predictions for the lower bound and upper bound of test results for the 271 suspected cases aboard the Diamond Princess
Drawing the Right Conclusions
There is another chapter to this story however. Whether the original group has 35 or 66 cases, these will not be the only 2019 n-Cov cases on board the Diamond Princess cruise ship, and it is crucial that policy makers understand why. The ship has nearly 3,700 people trapped on board, and the infection spread uninhibited for at least seven days. The correct conclusion is that the incubation period is long, and the doubling rate is short – therefore when these initial 271 passengers were selected and tested, there already existed another group of people who were infected and not symptomatic. This is important for three reasons:
- Don’t blame the quarantine. As additional cases are found over the next 10 days, it would be incorrect to assume that quarantining people to their rooms failed. That was the correct move and will prevent additional infections and serious illness.
- The “hidden population” of 2019 n-Cov is a crucial aspect of understanding this disease. This was the main point in the post published on Monday – that the undercount of this disease will hamper attempts to control the spread because of the long incubation period and asymptomatic cases. If policy-makers can draw the right conclusions from the Diamond Princess experience, it could dramatically help in the effort to slow or stop the spread of the disease.
- It is likely that additional cases may have gotten off the ship between 1/20 and 2/2, and those passengers should be alerted and local health officials made aware of the risk.
We will publish a follow up article to this once the test results for the 271 passengers are completed. Our initial estimates are that at least 100 people will test positive before the quarantine is released. We estimate that even if quarantine efforts prove perfectly successful, the Diamond Princess will likely have over 100 people aboard the ship test positive for 2019 n-Cov before the quarantine is released.
Learn how to start measuring variables the right way – and create better outcomes – with our two-hour Introduction to Applied Information Economics: The Need for Better Measurements webinar. $100 – limited seating.

